A Normal Density Curve Has Which of the Following Properties

Understanding the properties of normal distributions means you can use inferential statistics to compare different groups and make estimates about populations using samples. 2 fX 1 2πσ2 exp x μ 2 2σ2.

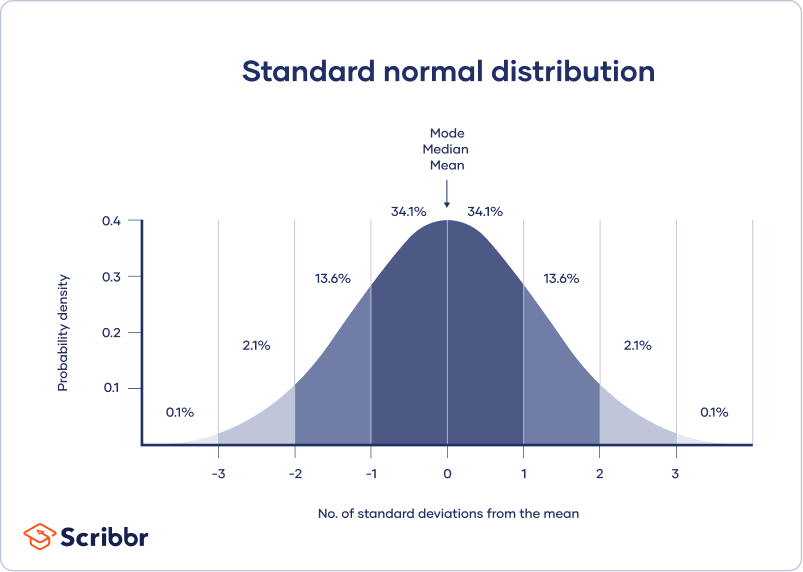
Normal Distribution Examples Formulas Uses

The normal curve is unimodal 3.

. D All of these choices are correct. The total area under the curve should be equal to 1. The maximum ordinate occurs at the centre 5.

Those parameters are the population mean and population standard deviation. 31 Properties of the Normal Curve A speci c normal curve is completely described by giving its mean and its standard deviation. A normal density curve has which of the following properties.

B It has a peak centered above its mean. 05 points A normal density curve has which of the following properties. It has a peak centered above its mean.

A normal density curve has which of the following properties. Properties of the Normal Curve. Option E is correct Why Join Course Hero.

You can fit a normal curve to your data using a probability density function. Course Hero has all the homework and study help you need to succeed. Properties of the Normal Density Curve 1.

The spread of the curve is proportional to the standard deviation D All of the answers are correct. The quartiles lie 1 standard deviation below and above the mean. B It has a peak centered above its mean.

Statistics and Probability questions and answers. You can multiply that number by 100 and say there is a 100 percent chance that any value you can. Some of the important properties of the normal distribution are listed below.

C The spread of the curve is proportional to the standard deviation. It is symmetric around the point which is at the same time the mode the median and the mean of the distribution. This article throws light upon the fifteen main principles of normal probability curve.

C The spread of the curve is proportional to the standard deviation. Keep these two facts in mind when you create or interpret density curves for different distributions. The normal curve is asymptotic to the X-axis 6.

Density curves have the following properties. Known characteristics of the normal curve make it possible to estimate the probability of occurrence of any value of a normally distributed variable. The total area under the graph of the equation over all possible values of the random variable must equal 1.

The mean and the median equal each other. The total area under the curve equals 1. The spread of the curve is proportional to the standard deviation.

They are symmetrical curves with the values concentrated in the center of the curve and fewer in the tails. The normal distribution belongs to a family of distributions that has the same shape. The normal distribution with density mean and standard deviation has the following properties.

The area under the curve is 1. Suppose that the total area under the curve is defined to be 1. It is symmetric with respect to its mean.

Properties of a normal density curve Symmetric and has a bell-shafted curve. 3 It has a pick centred above its mean. A normal density curve has which of the following properties.

Some of the properties are. C The spread of the curve is proportional to the standard deviation. In a probability density function the area under the curve tells you probability.

It has inflection points at mean-1 standard deviation and mean 1 standard deviation. Many professional schools require applicants to take. D All of the above.

A It is symmetric B It has a peak centered above its mean. The equation must satisfy the following two properties. It is bell-shaped where most of the area of curve is concentrated around the mean with rapidly decaying tails.

10 Points It is symmetric The spread of the curve is proportional to its standard deviation. The normal curve is symmetrical 2. The area under the curve always adds up to 100.

Because meanmedianmode the curve has a single peak and the highest point occurs at xmean 3. B It has a peak centered above its mean. Determine whether each of the following statements regarding a Normal density curve is true or false.

A It is symmetric. The mean median and mode of the distribution coincide. The normally distributed curve should be symmetric at the centre.

The standard deviation xes the spread of the curve. It is symmetric about the mean 2. The curve will never dip below the x-axis.

Referred to as a normal distribution Gaussian Distribution. The normal curves are a family of symmetric single-peaked bell-shaped density curves. A normal density curve has which of the following properties.

D All of the above. It has two parameters that determine its shape. The density curve always lies on or above the horizontal axis.

Write a function that gives the total cost rt in dollars of ebukas rent if he pays it t weeks late. It is symmetric it has a peak centered above its mean the spread of the curve is proportional to its standard deviation. Characteristics of Normal Density Curve 1 It is symmetric in nature 2 The spread of the Normal distribution curve is proportional to the standard deviation.

A It is symmetric. A Normal density curve has which of the following properties. In a normal distribution the mean mean and mode are equalie Mean Median Mode.

Mean median and mode coincide 4. If ebuka pays the rent late his landlord charges 4 interest per week that the payment is late. The height of the graph of the equation must be greater than or equal to.

A It is symmetric. Statistics and Probability questions and answers. Additional Resources Introduction to Relative Frequency Histograms How to Make a Bell Curve in Excel.

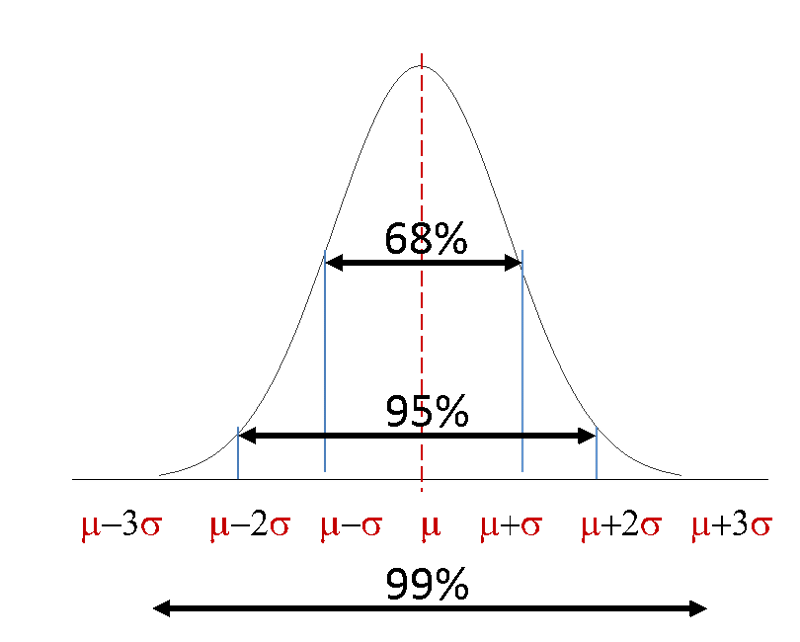
Calculate the z-score given the mean and SD Subtract the mean and divide by the standard deviation. All of the properties mentioned in the other choices are correct It has a peak centered above its mean. It is symmetric it has a peak centered above its meana and the spread of the curve is proportional to its standard deviation Control groups are used in experiments in order to.

Ebukas monthly rent is 750. A Normal density curve has which of the following properties. A probability density function is an equation used to compute probabilities of continuous random variables.

The shape is described by the following expression.

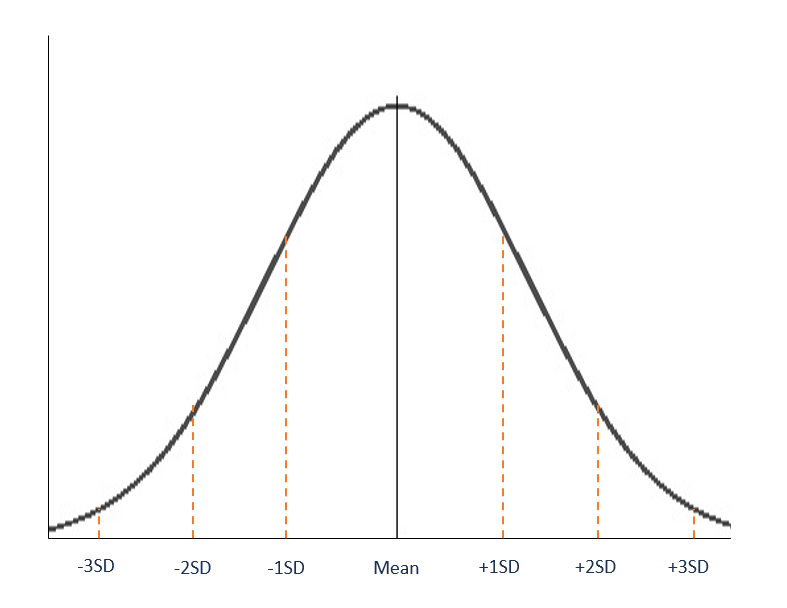
Normal Distribution Overview Parameters And Properties

Normal Distribution And Z Scores Explained Introductory Statistics Statistics Math Statistics Notes Normal Distribution

Characteristics Of A Normal Distribution